Real World Math
Kuchenstück halbieren
Wie man ein Kuchenstück der Länge nach halbieren muss, ist klar. Aber wenn man es quer teilen möchte, wo muss man schneiden, damit beide Teile gleich groß sind? Ein reales Mathe-Problem bei Kaffee und Kuchen.
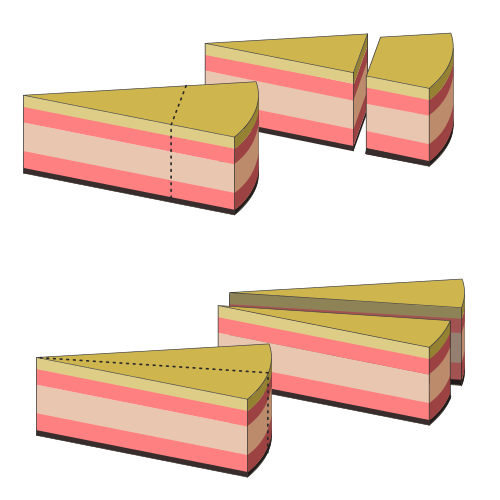
Da sitzt man zu zweit gemütlich im Café und kann sich nicht recht entscheiden. Die Lösung: Man bestellt zwei Stück Kuchen und jeder bekommt von beiden die Hälfte. Wer allerdings schon mal versucht hat, eine 3 km hohe Sahnetorte zu halbieren, wird mir zustimmen: Vom Rand zur Spitze schneiden ist fast nicht durchführbar. Also quer schneinen. Aber wo schneidet man wenn der vordere Teil viel dünner, als hinten? Sicherlich nicht in der Mitte...
Mathematische modellierung des Problems
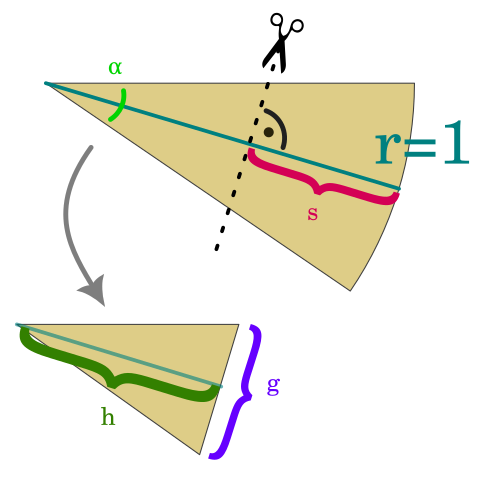
Um dieses Problem zu vereinfachen, gehe ich davon aus, dass das Kuchenstückes gleichmäßig strukturiert ist und nicht etwa Erdbeeren nur im hinteren Teil sind oder ein Teigrand an der Basis unattraktiv ist… Zudem können wir sagen, dass ein Kuchenstück von oben gesehen ein Kreissektor ist. Daher werde ich nur eine Fläche betrachten. Ein Kuchen wird wird üblicherweise in 8, 12 oder 16 Stücke geteilt. Die letzte Vereinfachung ist, einen Kuchen mit Radius 1 zu betrachten. Würde man den Radius mit in die Rechnung nehmen, würde er sich ohnehin herauskürzen.
Grundlegendes
Ich suche also `s`, den Abstand vom Kuchenrand, an dem ich das Messer ansetzen muss. Das ist abhängig vom Winkel des Kuchenstückes, also von der Anzahl der Kuchenstücke.
Terme für die Flächen aufstellen
Ich stelle einen Term für das ganze Kuchenstück, sowie für das abzuschneidende Stück. Der Einfachheit halber berechne ich das Stück an der Spitze, denn hierbei handelt es sich um ein gleichschenkliges Dreieck.
Die Bedingung als Gleichung schreiben
Damit die Dreiecksfläche am Ende die Hälfte der Gesamtfläche ist, formuliere ich diesen Zusammenhang in einer Gleichung. Diese Gleichung löse ich nach s, der gesuchten Schnittposition.
Konkretes Beispiel
Ich berechne die Schnittposition für einen Kuchen mit 12 Stücken.
Der Schnitt muss also bei etwas weniger als einem Drittel vom Kuchenrand her gesetzt werden.
Für andere Kuchen-Teilungen
Bei anderen üblichen Kuchenteilungen ist der Unterschied nur minimal:
| Teiler `k` | Schnittposition `s(k)` |
|---|---|
| `k=4` | `s_4 ~~ 0,3733` |
| `k=8` | `s_8 ~~ 0,3115` |
| `k=12` | `s_12 ~~ 0,3011` |
| `k=16` | `s_16 ~~ 0,2975` |
| `k=20` | `s_20 ~~ 0,2958` |
| `k=100` | `s_100 ~~ 0,293` |
Alternative Überlegung 1 (ungenauer, ganzer Kreis)
Wenn man den ganzen Kuchen betrachtet, bilden alle diese Schnittkanten
ein Vieleck – vielleicht annähernd einen Kreis.
Die Fläche des inneren Kreises sollte dann die Hälfte des gesamten Kreises sein.
`A_"groß" = pi * r^2`
`A_"klein" = pi * {:r_2:} ^2`
`2 * A_"klein" = A_"groß"`
`2 * pi * {:r_2:} ^2 = pi * r^2`
`r=1; r_2 = 1-s`
`2 * cancel(pi) * (1-s)^2 = cancel(pi)`
`(1-s)^2 = 1/2`
`1-s = sqrt(1/2)`
`s = 1-sqrt(1/2) ~~ 0,2929`
Das ist interessanterweise genau der Grenzwert von oben.
Alternative Überlegung 2 (ungenau, Dreiecksmodell)
Wenn man das Kuchenstück vereinfacht als ein Dreieck betrachtet, kann man das Problem
unter Anderem mit dem Strahlensatz lösen.
Wir setzen den Radius des Kuchens (die Höhe des Dreiecks) gleich auf `1`.
Über den Strahlensatz ermittle ich die Grundseite des kleinen Dreiecks, in Abhängigkeit vom großen Dreieck und der Schnittposition:
`g_1 / 1 = g_2 / {1-s}` d.h. `g_2 = g_1*(1-s)`
Ich stelle Formeln für die beiden Dreiecksflächen auf und baue dabei den Zusammenhang zwischen `g_1` und `g_2` ein:
`A_"ganz" = 1/2*g_1`
`A_"Spitze" = 1/2*g_2*(1-s) = 1/2* g_1*(1-s) * (1-s) = 1/2 * g_1*(1-s)^2`
Das gewünschte Verhältnis der Flächen als Gleichung:
`2 * A_"Spitze" = A_"ganz"`
`cancel(2) * (1/cancel(2) * cancel(g_1)*(1-s)^2) = 1/2*cancel(g_1)`
`(1-s)^2 = 1/2`
`1-s = 1/sqrt(2)`
`s = 1 - 1/sqrt(2) ~~ 0,2929`
Es kommt also exakt der gleiche Wert heraus, wie bei der Überlegung mit dem ganzen Kreis.